De Analysi Promota & Key Letters from Commercium Epistolicum
The following texts are my translations of selected writings from the Newton-Leibniz correspondence (from the edition of Collins, John. Commercium Epistolicum de Analysi Promota. Paris: J. B. Biot, 1856). I had produced them in 2010 in order to both learn Latin and to familiarize myself in detail with the 18th Century calculus debates, in preparation for my translation of Jean d'Alembert's Calcul différentiel and Equation différentielle.
I've made minor adjustments in order to present these texts online, but the current document preserves overall my traversal - as a Latin neophyte - of the key "evidence" cited by d'Alembert in his discussion of the inventor(s) of the calculus.
The act of proceeding to translate these works as someone quite new to Latin is then a gesture that alternatively envisions humanities production processes. The 21st century humanities scholar may be seen to bring general hermeneutical competencies to his or her projects, applying a readerly / writerly subjectivity to historical works that need to be addressed, whether they deal with mathematics or are texts of high historical science encoded in the lingua franca of a previous age.
From the letter of Newton to Collins, 1672, 10 Dec.
Because I am inspired to praise as thus far satisfying the lections Mathematicis of our revered friend Mr. Barrow, I am more than pleased to accept their (Slusse and Gregory's) request to me to write concerning the Tangentes Methodum.
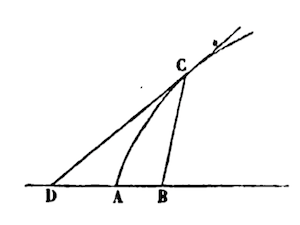
With what kind of demonstration shall we start? Take CB next to AB, at any given angle, closed by the curve AC, and call AB x, and BC y, and make the relation between x and y expressed by any equation you please, say x^2 - 2xxy + bxx - bbx + byy - y^2 = 0, for the curve alone. Multiply the terms of the equation by any arithmetic progression nearly y dimensions, say x^3(0) - 2xxy(1) + bxx(0) - bbx(0) + byy(2) -y^2(3) almost to x dimensions, say x^3(3) - 2xxy(2) + bxx(2) - bbx(1) + byy(0) - y^2 (0).
The first product will be the Numerator, and the last, divided by x, the Denominator, i.e. what is expressed by the length BD to the end D being the tangent CD: it is therefore the length BD = -2xxy + 2byy - 3y^3 / 3xx - 4xy +2bx -bb. This is a particular if not better corollary to the general Method, where it is extended short of any tiresome calculation, in not only considering Tangents to any curve in Geometry or Mechanics, but even in considering other straight lines. It certainly reveals other hidden problems, of curvature, area, length, curved centers of gravity, etc. Not (as in Huddeni's method of Maximum and Minimum) but in drawing up the former equations, which are immune to surd quantities.
This method interwoven with yours, then any exegetical equation I put forth, I shall reduce to an infinite series. I recall Barrow once told me, explaining the work I was reading, to consider this matter of the method of tangents: However, from this work I was unaware of what to take away.
I trust my brief public consideration of Slusse's method of tangents: to the greatest possible extent he has come to the same model, you should send it to me lest I fail to consider it.
No. XLVIII. Previous letter of Isaac Newton, Professor of Mathematics of the celebrated Cantabridgian Academy, to Henrick Oldenberg, secretary of the Royal Society of London.
June 13, 1676, with the illustrious, courageous Gottried William Leibniz (eo mediante) joining in. Received by Oldenburg and sent to Leibniz June 26th.
Though modest Leibniz is, in the excerpt from the letter he sent to me he should grant much to us concerning a certain speculation on the Infinitarum Serierum, what has now become rumor: yet he grants not too much in what he claims, a method to factor any quantity of such a series, not to mention a different shorthand he devised resembling - if not improving upon - ours.
Since his invention has come to be known to the English, and about which he had written some years before this Speculation: to grant this somewhat out of what he has satisfactorily acquired are several advances which occurred to myself, about which I send you.
Fractions in an infinite series may be factored by division, and radical quantities by extracting the radicals, in the same way as yours are employed in appearance, and by custom of decimal notation. They are fundamental to this factoring.
Yet many extractions of radicals may be abbreviated by this * Theorem. P + PQ m/n = P m/n + m/n(AQ) + m -n / 2n (BQ) + m - 2n / 3n (CQ) + m - 3n / 4n (DQ) + etc.
Whereby P + PQ signifies the quantities of that root, which can be any dimension, or root dimensions to be investigated. P is the principal terms of these quantities, Q represents terms left divided by the first. And m/n is a number indicating the dimension of P + PQ, either the dimension it is integrated with, or, (so to speak) a fraction; either affirmative or negative.
For, in the same way, to analyze, for aa, aaa, etc. one is in the habit of writing a2, a3, etc. , so I, for (square root of) a, a3 c.a5, etc. write a1/2, a3/2, a5/3, and for 1/a, 1/aa, 1/aaa, write a-1, a-2, a-3. And so for aa / (sqrt(c.a3 + bbx)) I write aa X (a3 + bxx)-1/3; and for aab / sqrt(c: a3 + bxx X a3+ bbx:) I write aab X (a3 + bxx)-2/3. So in the final case, as (a3 + bxx)-2/3 would be P + PQ m/n gives the rule written P = a3, Q = bbx / a3, m = -2, n = 3. Finally for the terms between the operands invented in such position, I use A, B, C, D, etc. Truly, we use A for the first term, P m/n B for the second devised here m/n(AQ); and so on. I will give examples for the rule used by the others.
Example 1. Suppose there were sqrt(cc + xx) ( or (cc + xx)1/2) = c + xx /2c - x4 /8c3 + x4/16c5 - 5x3/128c2 + 7x10 / 256c9 - etc. For, in this case, it is P = cc, Q = xx /cc, m = 1, x = 2, A (= Pm/n = cc1/2) = c. B (=m/n(AQ)) xx/2c, C (=m-n/2n(BQ)) = -x4/ 8c3 And so on.
Example 2. Suppose sqrt(5: c5 + c4x - x5) : (that is, (c5 + c4x - x5)1/5 = (c + c4x - x5) / 5c4 - (2c3xx + 4c?x4 - 2x10 )/ 25c3 + etc. To show this, I substitute, in using rule 1 for m, 5 for n, c3 for P, and c4x - x5 / c5 for Q. It could be -x5
* In 1669, Newton made well known, binomial resolution by this series with the analysis printed above, page 19, line 19,20.1 1. On page 73, line 23. [F. L.]
substituted for for P, and c4 + c5 / -x5 for Q. And then avoiding sqrt(5:c5 + c4 - x5: = -x + (c4x + c5 )/ 5x4 + (2c2xx + 4c3x + c10 )/ 25x9 + etc. The first means is to be chosen if x is very small; the last if very large.
Example 3. Suppose there be N / sqrt(c:y3 - a2y) (that is, N x (y3 - a2y) -1/3) equal to N x 1/y + aa / 3y3 + 2a4/9y5 + 14a5/81y2 etc. For P = y3. Q = -aa/yy. m= -1, n = 3. A (Pm/n = y3x-1/2) = y -1, that is 1/y. B(=mn(AQ)=-1/3 X 1/y X -aa/yy) = aa/3y3 etc.
Example 4. Cube root from its quadruple square d + e, (that is (d + e)4/3) is d4/3 + 4ed1/3 / 3 + 2ce / 9d2/3 - 4e2/ 81d3/2 + etc. For, P = d. Q = e/d. m =4. n = 3. A(=Pm/n) = d4/3 etc.
Example 5. The same, but only if a single power is drawn out. If its quadruple cube is d + e (that is, (d + e)3 or (d + e)5/1) would remain : it will be close to the rule, P = d. Q = e/d . m = 5 and n= 1. Thus so far A (=Pm/n) = d3. B (= m/n(AQ)) = 5d4e, and so C = 10d2ee. D = 10dde3. E = 5de4. F = e4, and G (=m-5n/ 6n (FQ)) = 0. That is (d + e)5 = d3 + 5d4e +10d3ee + 10dde3 + 5de4 + e5.
Example 6. But likewise, if it is simple, or has been repeated, coming to complete the rule. So if 1 / d + e (that is, (d + e)-1 or (d + e) -1/1) it will end in a simple series and be resolved: it shall be close to the rule, P = d. Q = e/d. m = -1 and n = 1, and A (= Pm/n = d-1/1) = d-1 or 1/d. B (=m/n (AQ) = -1 X 1/d X e/d) = -e/dd. And so C = ee/d3. D = -e3/d5 etc. That is, 1 /d + e = 1/d - c/dd + ee/ d2 = e3/d4, etc.
Example 7. So now (d + e)-2, (that is united three times by d + e, even once by this cube) avoids 1/ d3 - 3e /d4 + 6ee /d5 - 10e3 /d6 + etc.
Example 8. And N X (d + e)-1/3, (that is N divided by the cube radical of d + e ) avoids N X 1 / d1/2 - e / 3d4/3 + 2ee / 9d7/3 - 14e3 / 81d10/2 + etc.
Example 9. And N X (d + e)-3/5 (that is, N divided by the quadruple cube radical from the cube of this d + e, or N / rt(5:d3 + 3dde + 3dee + e2) avoids N X 1/ d3/2 - 3e / 5d3/2 + 12ee / 25d13/3 - 52e3 / 125d13/5 + etc.
From this rule, generating powers, dividing by powers or by radical quantities and other extractions of radicals in numbers, is now easy to accomplish.
Extractions of Radicals. The affected equations appear to imitate numerical extraction. In fact, the methods of Vietae and Oughtredi, minus this annoyance, are suitable for ours. What else can be devised to show this, without repeating this model?, see Tractatu de Analysi, etc., pag. 9, 10, etc 1.
I shall say enough to bring it forth, up to taking the root of any equation and extracting it once, for the rule resolving similar equations can thus be preserved; taking any one from many rules of this sort, one may commonly form a general rule; and since every root, whether simple or affected, can be extracted in infinite ways from any simple expression, this is always advised.
From equations reduced to infinite series, how may areas and curved longitudes, taut and solid surfaces, even any segment of any shape, its center of gravity, be determined, and how can every mechanical curve be reduced to an equation for an infinite series, thus to be solved as if it were a problem of geometry? This would take too long to describe. The model would be sufficient if it could enumerate so great a problem : You say the same, thankfully, the letters, A, B, C, D, etc., for the terms of the series, as I sometimes admit using.
1. If from the given straight sinus, or from the bent sinus, we want an arc: let there be a radius r and a straight sinus x: there shall be an arc = x + x3 / 6rr + 3x5 / 40r4 +5x1 / 112r8 + etc. That is, = x + (1 X 1 X xx) / (2 X 3 X rr) A + (3 X 3xx) / (4 X 5rr)B + (5X 5xx) / (6 X 7rr)C + (7 X 7xx) / (8 X 9rr) D + etc. Suppose d were a diameter, and x a bent sinus, and the arc will be d1/2x1/3 + x3/2/ 6d1/2
See page 61 and following, and the supplement of the Comm. Epist.
+ 3x3/2 / 40d3/2 + 5x1/2 / 112d3/2, etc. That is, = sqrt(dx) in 1 + x/6d + 3xx/40dd + 5x3 / 112d3 + etc.
2. If in turn, from the given arc we want a sinus, let there be a radius r, and an arc z: the straight sinus will be = z - z3 / 6rr + z5 / 120r4 - z7/5040r6 + z9/36z88or8 - etc. That is, = (z - zz) / (2 X 3rr) A - zz / 4 X 5rr B - (zz / 6 X 7rr) C - etc. And the bent sinus = zz /2r - (z? / 24r3) + (z? /720r5) - (z? / 40320r7) + etc. That is, zz / 1 X 2r - zz / 3 X 4rr (A) - zz / 5X 6rr (B) - zz / 7 X 8rr C - etc.
3. If the chosen arc is in a given ratio to the other arc, its diameter = d, the chord of the arc = x, and the desired arc to this given arc goes from n to 1 : The chord of the desired arc will be = nx + (1 -nn / 2 X 3dd)xxA + (9 - nn / 4 X 5dd)xxB + (25 - nn / 6 X 7dd)xxC + (49 - nn / 8 X 9dd)xxD + (81 - nn / 10 X 11dd)xxE + etc.
Whereby it is noted that because n has an uneven sum, the end of the series is infinite, and it will similarly be multiplied, avoiding any (sum) produced by common algebra, giving an angle for this number, n.
If on axis AB of two in the ellipse ADB (with center C, and another axis DH) were to be given any point E, at the tip of line EG, and were it to pass through G, bearing angular movement, and having given the area of the elliptical section BEG, the line GF should be found, by the point G descending to the normal axis: BC = q, DC = r, EB = t, and the area doubled = z.
And GF will be = z/t -(q/6rrt4) z3 + (10qq -9qt / 120r4t7)z5 - 280q3 + 504qqt - 225qtt / 5040r8t10 (z7) + etc.
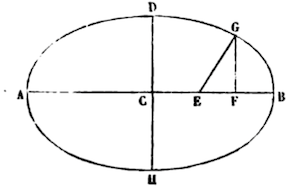
And so the astronomical problem of Kepler can be solved.
5. In the same ellipse, if we establish CD = r , CB2 / CD = c and CF = x The elliptical arc DG will be = x + 1/6cc (x3) + 1/10rc3 (x5) + 1/14rrc4 (x7) + 1/18r3c4 (x9) + 1/22r4c6 (x11) + etc.
- 1/40c4 - 1/28rc4 - 1/ 24rrc4 - 1 / 22r3c7 + 1/112c5 + 1/48rc7 + 3/88rrc8 - 5/1152c8 - 5/352rc9 + 7/2816c10
1 To be exact, one must write: - 280q3 - 504q2t + 225qt2 / 5040r6t10 (z?) [ Remark by Horsley.]
Here the terms of higher numerical coefficients (1/6, 1/10, 1/14 etc.) occur in a musical progression: And all lower numerical coefficients in any one column will continuously multiply higher numerical coefficients ending in these final progressions 1/2n -1 / 2 , 3/3n - 3 / 4, 5/4n - 5 / 6, 7/5n - 7 / 8, 9/6n -9 / 10, etc. Whereby n signifies a numerical dimension , actually c in the denominator of this higher term. E. g. for the numerical coefficients coming below 1/22r4c, I put n = 6, similarly 1/22 (the actual numerical coefficient 1/22r4c4) in 1/2n-1 / 2, that is, in 1; and terms of numerical coefficients go next to the lower : then I consider 1/22 in 3/3n - 3/ 4, or in n - 3 / 4, that is, in 3/4: and the third term of the numerical coefficient 3/88 goes in that column. Moreover, this 3/88 X 5/4n - 5 / 6 produces the fourth term of the numerical coefficient, 5/ 352; and 5/352 X 7/5n - 7 / 8 produces 7/2816 the lowest term. Similarly, in the other at every point of the column it keeps appearing: it approaches the actual value DG is produced by this very pleasing rule.
In this regard, if BF is designated x, is as r on the straight side of the ellipse, and e = r / AB. It shall be an elliptical arc
BG= sqrt(rx) in ____________________________________________________ 1 + 2 -2 +4 -10 -1/2e x + 3e x2 -9e +30e ------- -5/8ee +23/4e2 x2 -123/4e2 x4 + etc. 3r _____ -7/16e3 +91/8e3 5rr ---------- -45/128e4 7r3 ------------- 9r4
How so, if the edge of the whole ellipse remains? CB bisected by F, and how does the arc DG do this via the earlier theorum, (the arc BG in the later?).
If on the other hand, out of the given arc of the ellipse DG, one wants that of CF, then I say, CD = r, CB2/CD = c, and this arc DG = z, CF will be =
z - 1/6cc(z3) - 1/10rc3 (z5) - 1/14rrc4(z7) - etc. +13/120c4 + 71/420rc5 - 493/5040c6
On the other hand, what part of the ellipse shall each be, easy to adapt to a hyperbola, changing as much as the signs c and e, whereby they are of unequal dimension.
7. In addition, suppose CE were a hyperbola, with an asymptote AD, AF established as a right angle FAD. On AD is raised a perpendicular BC and DE passing through the hyperbola at C and E. Let AB be a, BC b, and the area BCED be z. BD will be = z/b + zz/2abb +z3/6aab3 + z4/ 24a3b4 + z5/120a4b5 + etc. Thereby the coefficients of the denominators I can multiply by terms of arithmetic progression, 1, 2, 3, 4, 5, etc. continuously. And out of the logarithm can come only the appropriate numbers.
8. Let VDE be a Quadratic, with a vertex V and A in the center, with AE, half the diameter of a circle, of any size, with a right angle VAE: and reaching back to AE, any perpendicular line DB, and the quadratic tangent DT passing through the axis AV at T: Let AV = a, and AB = x. DB will be = a - xx/3a - x4/45a3 - 2x4/945a5 - etc. And VT = xx/3a + x4/15a3 + 2x6/189a5 + etc. And the area AVDB = ax - x3/9a - x5/225a3 - 2x7/6615a5 - etc. And arc VD = x + 2x3/27aa + 14x5/2025a4 + 604x7/893025a6 + etc.
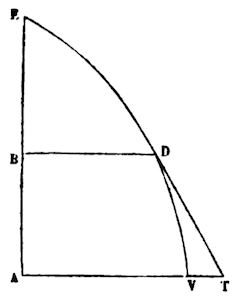
From which, BD, or VT, or rather, the area AVDB, the arc VD, by the resolution made by the equation it can be, in turn, x or AB.
9. And finally, in the spheroid AEB, the ellipse AEB turns around the given axis AB, and divides the lesser plane, AB by the transverse axis, DG parallel to AB, CDE the perpendicular, bisecting axis, and FG is parallel to CE. Let CB = a, CE = c, CF = x, and FG = y: now the spherical segment CDGF, said to include the lesser plane, would be:
+ 2xcy - x/3c(y3) - x/20c3(y5) - x/56c5(y7) - 5x/576c7(y9) - etc. - cx3/3aa - x3/18caa - x3/40c3aa - 5x3/336c5 - etc. -cx4/20a4 -x4/40ca4 - 3x4/160c3a4 - etc. - cx7/56a4 - 5x7/336ca4 - etc. - 5cx9/576a8 - etc. - etc.
Thereby, the numerical coefficients of the higher terms (2, -1/3, -1/20, -1/56, -5/576, etc.) extended infinitely, I multiply the first coefficient 2 and then continue with these terms of the progression -1 X 1/ 2 X 3, 1/X3/ 4 X 5, 3 X 5/6 X 7 5 X 7/8 X 9, 7 X 9/10 x 11, etc. And the numerical coefficients of the terms in each column infinitely descend, the continuously multiplied coefficient of the greater terms being extended in the first column by the same progression; in the second, by terms such as 1 X 1/2 X 3, 3 X 3/4 X 5, 5 X 5/6 X 7, 9 X 7/8 X 9, etc. in the third column by the terms 3 X 1/2 X 3, 5 X 3/ 4 X 5, 7 X 5/ 6 X 7, 9 X 7/8 X 9, etc.; in the fourth by the terms 5 X 1/2 X 3, 7 X 3/4 X 5, 9 X 5/ 6 X 7, etc; in the fifth, by the terms 7 X 1/2 X 3, 9 X 3/4 X 5, 11 X 5/6 X 7, etc. and so on in infinitum.
And in the same way, the segment of the other solid figure may be sketched, and the same values may at any convenience be infinitely produced by a series of any numerals.
From these analyses, it is seen that many finite quantities are amplified by such infinite equations: indeed by which they can be extended in a sense to all the problems indicated (excepting Diophantine and similar numerals).
All of them may not be so universally derived, nor shall any other methods elicit infinite series. For there are some problems in which a simplicity of impression is not permitted to come through to an infinite series by division or extraction of roots. How one may then proceed in this case, I am not permitted to say; Nothing other may then be drawn out concerning the reduction of infinite series where the nature of things shall come forth from the mind. Yet, I write sparingly because these speculations shall begin to give me daily scorn, so much that I have kept away from them for five years.
I should add one more thing: for after the problems are elaborated from these equations to infinity, were the approximations then to vary in mechanical uses, I'd manage to cause to be formed none at all, and much labor and time would out of habit become necessary for me to expend by the other methods in question.
Any of these could be examples from Huygen's Tractatus and the other works on quadratures of the circle. For, coming out of the given arc is chord A, and half of this arc chord B, immediately following it; Pretend this arc is z, and the radius of the circle, r, and next to that above will be A (certainly the sinus of z halved in two) = z3 / 4 X 6rr + z4 / 4 X 4 X120r3 - etc. And B = 1/2z - z3 / 2 X 16 X 6rr + z5 / 2 X 16 X 16 X 120r4 - etc. Consider now B in a fictitious number n, and remove A by the product, so that the remaining second term ( certainly - nz3 / 2 X 16 X 6r + z3 / 4 X 6rr3 ) shall consequently disappear, making it = 0, and then n shall become = 8 and be 8B - A = 3z * - 3z4 / 64 X 120r4 + etc. That is, 8B - A / 3 = z and so z2 / 768r4 - etc. shall erroneously exist in excess. This is Huygen's theorem.
Above, if in arc Bb you expand forward an undefined AD towards point G, by any straight (actae) GB, or Gb nearly equal to this arc. We have the center of the circle C, diameter AK = d, and the widened AD = x: and it will be DB (= sqrt(dx - xx) = d1/2 x1/2 - x3/2 / 2d1/2 + x3/2 / 6d1/2 + 3x5/2 / 40d3/2 + 5x7/3 / 112d5/2 etc. And AE - DB:AD::AE:AG. Whereby AG = 3/2d - 1/5x - 12xx / 175d + or - etc. Imagine then AG = 3/2d - 1/5x: and in turn, DG will be (3/2d - 6/5x): DB::DA:AE - DB. Whereby AE - DB = 2x3/2 / 3d1/2 + x3/2 / 5d3/2 + 23x7/2 / 300d5/2 + etc. Add DB, and produce AE = d1/2 x1/2 + z3/2/ 6d3/2 + 3x5/2 / 40d3/2 [+] 17x7/2 / 1200d3/2 + etc.
DE ANALYSI PER AEQUATIONES NUMERO TERMINORUM INFINITAS.
General method by which any curved magnitude will be measured by Infinite series thought out once, by a sequence more briefly explaining what you have carefully demonstrated.
At the base AB of any curve AD, add a perpendicular line BD: and make AB = x , BD = y, and a, b, c, etc. be given magnitudes, and m, n, whole numbers.
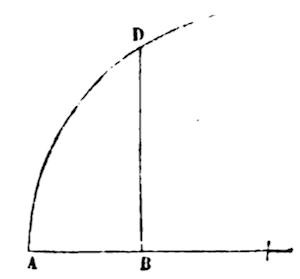
Simple, Squared Curve
REG I. If axm/n = y; let an / m +n (xm+n/n) = Area ABD.
1. If x2 (=1x2/1) = y, that is, a = 1 = n, and m = 2. Let 1/3x3= ABD.
2. If 4 sqrt(=4x1/2)= y, let 8/3x3/2(=8/3sqrt(x3) = ABD.
3. If rt(3, x5)(=x5/3) = y, let 3/8x8/3(=3/8 rt(3, x5) = ABD.
4. If 1/x2 (= x-2) = y, that is, if a = 1 = n, and m = -2,
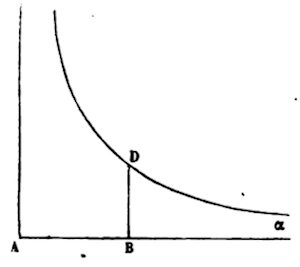
Let (-1/1x-1/1=) -x-1(=-1/x) = (alpha)BD, infinitely extending any negative segement towards (alpha), since it comes out of the other segement of line BD
5. If 1/ sqrt(x3) (=x -3/2) = y, let (-2/1x -1/2=)2/- sqrt(x) = BDa.
6. If 1/x(=x-1) = y, let 1/0x0/1 = 1/0x0= 1/0 X 1 = 1/0 = Infinity, which is like the area of the hyperbola coming out of each part of the line BD. [GB Note fluxion]
Composite Quadratic Curves from Simple Ones
REG II. If the value y is constructed out of many such terms, (no III) the Area will also have been constructed from areas emanating out of a single term.
First Example.
If x2 + x3/2 = y, let 1/3x3 + 2/5x5/2 = ABD. And indeed, if x2 is always = BF, and x3/2 = FD, from the preceding rule, let 1/3x3 = equal the surface AFB traced by the line BF, and let 2/5x5/2 = AFD be traced by DF. Whereby 1/3x3 + 2/5x5/2 = ABD as a whole.
So, if x2 - x 3/2 = y, let 1/3x3 - 2/5x5/2 = ABD.
And if 3x - 2x2 + x3 - 5x4 = y, let 3/2x2 -2/3x3 + 1/4x4 - x5 = ABD
Second Example.
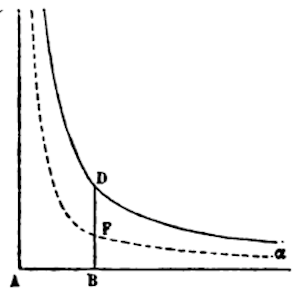
If x-2 + x-3/2 = y, let -x-1 - 2x-1/2 = (alpha)BD.
Or if x-2 - x-3/2 = y, let -x-1 + 2x -1/2 = (alpha)BD.
If any sign changes it will have a positive value (x-1 + 2x-1/2 or x-1 - 2x-1/2) for the surface (alpha)BD, in a manner such that it falls squarely on the base AB(alpha).
But if some part falls below ( which happens with a curve arranged crosswise along its own base between B and (alpha), to the point seen at δ, this is subsumed by the higher part, and will have a different value: To find their true sum, find both surfaces separately and add them. In addition to these examples, the rule has others I'd like to mention.
Third Example.
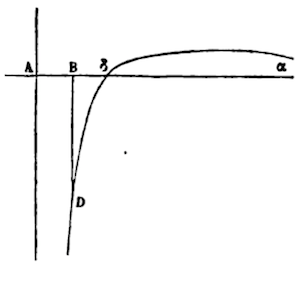
If x2 + x-2 = y, let 1/3x3 - x-1 = the delineated surface. I mention what you call the upper layers, constructed here coming horizontally out of the opposite side of line BD.
Of course, I should make x2 = BF, and x-2 = FD; therefore, let 1/3x3 = ABF, a surface traced by BF, and -x-1 = DF(alpha) a surface traced by DF. And this always happens to the indices (m + n / n), ratio of base x in the value of the desired upper layers, which would affect different signs. In this case, any part of surface BDδβ you shall divide only what you can (with infinite surfaces on both sides) and thereby construct the layers.
Subtract the surface reaching up from the smaller base Aβ; at the surface reaching up from the major base AB, you will have a different surface, βBDδ standing on the base. Just as in this example.
If AB = 2, and Aβ = 1, let βBDδ = 17/6:
Because the surfaces reach up to AB (viz. ABF - DF(alpha)) let there be 8/3 - 1/2 or 13/6, and for surfaces reaching up to ABβ (viz. Aσβ - δσ(alpha) let there be 1/3 - 1, or -2/3: and their difference will be (viz ABF - DF(alpha) - A(sym)β + δσ(alpha) = βBDδ 13/6 + 2/3 or 17/6.
In the same way, if Aβ = 1, AB = x, let βBDδ = 2/3 + 1/3x3 - x -1
So if 2x3 - 3x5 - 2/3x-4 + x-3/5 = y, and Aβ = 1,
Let βBDδ = 1/2x4 - 1/2x6 + 2/9x-3 + 5/2x2/5 - 49/18.
Finally, to note if the magnitude x-1 can be discovered in the value y, this term (having generated a hyperbolic surface) is separated as in the next consideration.
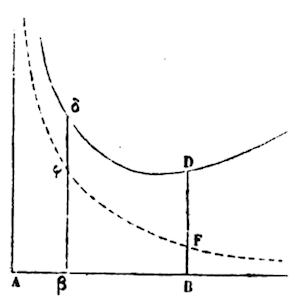
While if x2 + x-3 + x-1 = y : Let x-1 = BF, and x2 + x-3 = FD, and also Aβ = 1. And let δσFD = 1/6 + 1/3x3 - 1/2x-2, as generated from the term x2 + x-2.
Whereby, if the surface βσFB remains (a hyperbola), from any given part, βBDδ as a whole will be given.
Any Other Square.
REG. III. But if this value is y, or if any term is preceded by a more composite one, it is reduced to simple terms. Working in letters in the same way as dividing decimal numbers in arithmetic, roots are extracted, and even the affected equations solved; a curved surface will be found out of these terms, and by the preceding rules, you can trace out the following ones.
Division Example
Let aa / b + x = y; The current hyperbola, truly curved. Now to equate its denominator to its (liberetur), I divide it so.
(b + x) aa + o (aa/b - aax/b2 + aax3 / b3 - aax3 / b4… aa + aax / b --------------- 0 - aax / b + 0 -aax/b - aax3/b2 --------------- 0 + aax2 / b2 + 0 + aax2 /b2 + aax3 / b3 ------------------ 0 - aax3 /b2 + 0 - aax3/b3 - aax4/b4 ---------------- 0 + aax4 / b4 etc.
And so this series of y = aa / b+ x, newly produces y = a2 / b - a2x/b2 + a2x2/b3 - a2x3 / b4, etc., in this way continuing infinitely. Indeed (by the second rule) the desired area ABDC will equal a2x / b - a3x2 / 2b2 + a2x3 /3b3 - a2x4 /4b4, etc. Likewise an infinite series with only a few of the terms used, will be sufficiently exact in any of its terms, only if x is any number less than b.
In the same way, if 1 / 1 + xx = y, dividing will produce:
y = 1 - x2 + x4 - x6 + x8, etc
Whence (by the second rule)
ABDC = x - 1/3x3 + 1/5x5 - 1/7x7 + 1/9x9, etc.
But if xx is used as the first divisor, like (xx + 1), it will produce x-2 - x-4 + -6 - x-8, etc. for the value y. Whence (by the second rule)
BD(alpha) = -x-1 + 1/3x-3 - 1/5x-5 + 1/7x-7, etc.
At first we proceed with x sufficiently small; Finally, with a sufficiently large substitution.
Finally if 2x1/2 - x3/2 / 1 +x1/2 - 3x = y. Dividing will produce:
2x1/2 - 2x + 7x3/2 - 13x2 + 34x5/2, etc., then ABDC = 4/3x3/2 - x2 + 14/5x5/2 - 13/3x3, etc.
Example of Root Extraction
If sqrt(aa + xx) = y, the root extracted shall be:
aa + xx ( a + x2/2a - x4 /8a3 + x6/16a5 - 5x8/128a7, etc. aa / 0 + xx xx + x4/4a2 ----------- 0 - x4/4a2 -x4/4a2 - x6/8a4 + x8 / 64a6 ------------------ 0 + x6/8a4 - x8/64a6 x6/8a4 + x6/16a6 - x10/64a8 + x12/256a10 ----------------- 0 - 5x8/64a6 + x10/64a8 - x12/256a10 etc. ……
Whence, in the equation sqrt(aa + xx) = y now produces, viz.
y = a + x2/2a - x4/8a3 + x6/16a5 - 5x9/128a7, etc.
And (by rule 2) The desired area ABDC will be = ax + x3/6a - x5/40a3 + x7/112a5 - 5x9/1152a7, etc. And this is a quadratic hyperbola.
In the same way, if we have sqrt(aa-xx) = y, the same root will be a - x2/2a - x4/8a3 - x6/16a5 - 5x8/128a7, etc.,
Indeed, the desired area ABDC will be equal to ax - x3/6a - x5/40a3 - x7/112a5 - 5x9/1152a7 etc.
And this is a quadratic circle.
8.,
But if we put sqrt(x - xx = y), where the root equals the infinite series x1/2 - 1/2x3/2 - 1/8x5/2 - 1/16x7/2 - 5/128x9/2, etc.
And the desired area ABD will equal
2/3x3/2 - 1/5x5/2 - 1/28x7/2 - 1/72x9/2 - 5/704x11/2, etc.
or x1/2 in 2/3x - 1/5x2 - 1/28x3 - 1/72x4 - 5/704x5, etc.
And this is how the area of the circle shall be squared.
If sqrt(1 + ax2) / sqrt(1 - bx2) = y (any quadrature gives the length of this elliptical curve).
Extracting either root produces
1 + 1/2ax2 - 1/8a2x4 + 1/16a3x6 - 5/128a4x8, etc
1 - 1/2bx2 - 1/8b2x4 - 1/16b3x6 - 5/128b4x8, etc.
And divided, as in decimal fractions, we have
1 + 1/2bx2 + 3/8b2x4 + 5/16b3x6 + 35/128b4x8, etc. + 1/2ax2 + 1/4abx-4 + 3/16ab2x6 + 5/32ab3x8, etc. -1/8a2x4 - 1/16a2bx6 - 3/64a2b2x8, etc. + 1/16a3x6 + 1/32a3bx8, etc. -5/128a4 x8, etc.
Indeed, the desired area x + 1/6bx3 + 3/4b2x5, etc.
+1/6ax3 + 1/0abx5, etc. -1/40a2x5,etc.
But I shall observe which operation is not rarely abbreviated by giving the prepared equation, as in drawing out the example, sqrt(1 + ax2) / sqrt(1-bx2) = y.
If either fractional part produces, by many sqrt(1 - bxx)
sqrt(1 + ax2 - abx4 -bx2 ------------------------ = y, 1 - bx2
and the rest of the task is completed by extracting the root of the numerator like so, and dividing by the denominator.
I trust, from (hisce) this way of sufficiently reducing any value of y, any root but that of the denominator would be a problem, and to see this, we have:
x3 + sqrt(x - sqrt(1 - xx)) / cbrt(ax2 + x3) - 5-rt(x3 + 2x5 - x2/3 / cbrt(x +x2) - cbrt(2x - x2/3)
= y in an infinite series of simple terms, and, by the second rule, any conceivable surface.
Example of Solving an Equation
Numerical Equations Producing a Solution
Because all difficulties in the equation lie hidden, any method I use in the equations, I will first demonstrate.
Let y2 - 2y - 5 = 0 be solved: and let 2 be some number minus any decimal with its own part differing by the desired root. Then I put 2 + p = y, and I substitute this very value into the equation, and now I therefore produce p3 + 6p2 + 10p - 1 = 0, any root p which shall be sought is to be added to the quotient : Truly (neglecting p3 + 6p2 as unimportant) 10p - 1 = 0, or p = 0, 1 is nearly correct. So, I write 0,1 in the quotient, and place 0,1 + q = p underneath, and so this value, when substituted first, then produces q3 + 6, 3q2 + 11,23q + 0,061 = 0.
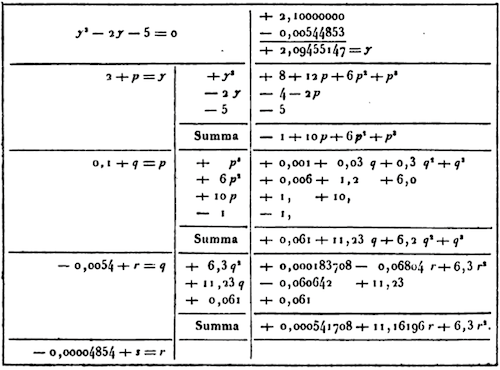
And with 11,23q + 0,061 nearly approaches correctness (veritati), or q almost equals - 0,0054 (certainly as long as the whole shape is given, I divide, if the first position of this shape and principal quotient remain exclusive) I write - 0,0054 below the quotient, when it is negative.
And suppose -0,0054 + r = q, as in the previous substitution, and this operation will produce a satisfying result. To be sure if up to two of so many shapes of so great a number in the quotient are now found once removed, an operation continually hoped for, in substituting q - 0,0054 + r in this 6,3q2 + 11,23q + 0,061, certainly this term is first (q2) because I shall ignore it and produce 6,3r2 + 11,16196r + 0,000541708 = 0, almost, or (rejecting 6,3r2)r = -0,0000541708 / 11,16196 = almost -0,00004853, which I write in the negative portion of the quotient. Finally, from the negative portion of the quotient up to the positive, I have 2,09455147, the desired quotient.
Otherwise nothing helps solve equations of several dimensions; they are raised from under the limit , if the first of these terms is gradually omitted.
Besides, it shall be noted that in any of these examples, if I doubt whether 0,1 = p truth is adequately near, for 10p - 1 = 0, were I to put 6p2 + 10p - 1 = 0, and the same root of this shape in the Quotient I might write, and the second or third quotient of the shape thus invites exploration, where in the equation is the resulting final quadratic coefficient of the penultimate term, not ten times more than any figure of the last term, which I then move into the coefficient of the antepenultimate term.
Labor shall be generally lessened, especially in equations of plural dimensions, if all desired shapes of the quotients are added, in a manner of speaking (dicto modo) (this is the lesser root to extract, out of the three final, newly resulting terms of the equation): it is indeed the way one gains, in these quotients, multiple duplicate shapes of whatever kind.
This method of solving equations I have unwittingly made known; certainly I considered it beforehand as remaining simple and easy to use. This demonstration will stand outside of my practice itself, as this work is easy to revoke afterwards.
Equations in which few or no terms are missing, will also generally facilitate their drawing, and equality may always be taken away: any single root with the acquired quotient will equalize the root of the equation first proposed. So I weigh this operation, equally able to institute it and in future arithmetic, most certainly withdrawing the quotient by the prime root of the equation (an analysis just as notable); the last equation or the same second or third final term would be thereby produced. Whatever labor is entailed, in this operation, one of the quantities will have been substituted in order to find another : you would resolve it differently, though still follow the quickest means I can fathom, especially when these numerical coefficients remain constant while being derived from multiple shapes.
Let p + 3 be substituted for y in (this) 4y3 + 5y2 - 12y + 17 = 0. And, with what you propose, it can be resolved through this form. *
y - 4 x y + 5 X y -12 X y + 17 = 0. A new equation will so generate p - 1 in p + 3 = p2 + 2p - 3. And p2 + 2p +2 in p + 3 = p2 + 5p2 + 8p + 6. et p3 + 5p2 + 8p - 6 in p + 3 = p4 + 8p3 + 23p2 + 18p - 18. and p4 + 8p3 + 23p2 + 18p - 1 = 0, which we seek.
The Given Equation Affecting a Solution
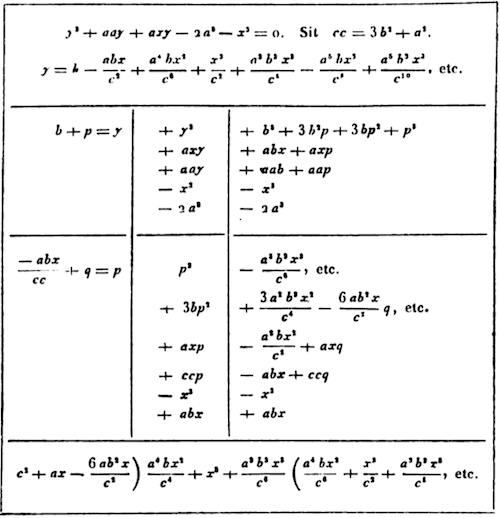
This is made clear in numbers: Let the given equation y2 + a2y - 2a3 + axy - x3 = 0, be solved.
First I ask if this value y with x is empty, that is, I bring out the root of the equation y3 + a2y - 2a3 = 0, and manage to get + a. And so I write + a in the quotient, and substituting + a + p = y, I substitute for y this same value, and the resulting terms (p3 + 3ap2 + 4a2p, etc.) I place near the margin. From which I assume the terms + 4a2p + a2x, where p and x are separately of minimum dimension, and the same almost equal non-existent ones shall be substituted, or, almost p = -1/4x, or p = -1/4x + q. And writing -1/4x in the quotient, I substitute - 1/4x + q for p. And so I then write the resulting terms in the margin, until I see them attached to the shape, and then I assume the quantities + 4a2q - 1/16ax2 , in which certainly q and x separately are of minimum dimension, and I devise something near q = xx / 64a, or q = + xx/64a + r; and I attach the quotient + xx/64a, substituting xx/64a + r for q, and then I proceed until it be satisfied.
* It is: {[(y - 4)y + 5]y - 12}y + 17 = 0 (F. L.)

But if I double multiple quotients of these terms, with one removed, now this one will be joined, should I wish: term one(q2), by having disregarded the new results of the equations, and this same, second part (-3/4 xq2), where x is as large as the penultimate quotient of the term. For the the remaining terms (3 aq2 + 4a2q etc.), inserting into the margin so that you may see, I substitute x3 / 64a + r for q; and out of the last two terms (15x4/4096a - 13t/128(x3) + 9/32x2r - 1/2axr + 4a2r) equations thus result, making a division 4a2 - 1/2ax + 9/32x2) + 131/128x3 - 15x4/4096a (I then bring out + 131x3 / 512a2 + 509x4 / 16384a3 , attaching the quotients.
Finally, these quotients (a - x/4 + xx/64a, etc.) by the second rule give ax - x2/192a + 13x4/2048a2 + 509x5/81920a3, etc. for the desired area, which approaches the truth much more closely, when the quantity x is tiny.
Another Method with the Same Solution
But if the value of so great an area should approach truth it will give a quantity x, when it is large. An example would be y3 + axy + x2y - a3 - 2x3 = 0. The solution then, selects the terms y3 + x2y - 2x3, in which x and y, separately or likewise multiplied, are both the greatest, and equal in every dimension. And from this semi-nothingness, I draw out an equal root. That is, I bring out x, and I write it as a quotient. But I extract what has similarly receded from y3 + y - 2 (unity substituted for x), this root which produces 1, and I multiply by x, writing it in the quotient. Finally I put x + p = y, and so I proceed as in the previous example, until I have the quotients x + a/4 + aa/64x + 131a3/512x2 + 509a4/16384x3, etc., precisely * area x3/2 - ax/4 + | aa/64x | - 131a3/512x - 509a4/32768x2, which you see in the third example of the second rule. Lucis freely gives this example for all those like the previous, making x and a themselves reciprocally substitutable there, and no other work would give an example of the solution to this joining.
But the area (xx/2 – ax/4 + |aa/64x| etc.) ends at any curve next to any asymptote gliding on forward; and the initial terms (x – 1/4a) values extracted from y, are always terminated at this asymptote. A portion of the asymptote is then easy to find. Likewise, this observation always goes with the area designating several terms that by division by x continues, practically because the asymptote of the rectangle curves however we consider the conical parabola - even by another, greater arrangement.
Still, this method requires omission, at least partially, because inapplicable curves orbiting around an elliptical form flex; altering the method by the example y3 + a2y + axy – 2a3 – x3 = 0, more clearly (of course, which of these dimensions themselves x will increase perpetually in quotients of the numerators, I will annotate next.
[* N. B. In the same sense that Newton makes use of the symbol |aa/64x|, Leibniz uses the symbol S aa/64x.] Addition.
If when the real value of y occurs, none should be formed along with x, if the quantities are surd or thoroughly unknown, they may be designated with that letter. So in the example, y3 + a2y + axy – 2a3 – x3 = 0 if this root y3 + a2y – 2a3 should have been surd or unknown, I will however produce (b) to set in its place, next bringing about the solution. Writing b in the quotient, I assume b + p = y, and I substitue y, as you can see. So now p3 + 3bp2, etc. will result, rejecting the terms b3 + a2b – 2a3, for which there is nothing equal; therefore since b is substituted, this root, y3 + a2y – 2a3 = 0. The next term, 3b2p + a2p + abx gives – abx/3b2 + a2 placed near the quotient, and -abx/3b2 + a2 + q is substituted for p, etc.
This operation complete, I assume another number for a, and y3 + a2y – 2a3 = 0, just as the numbers of the equations are more clearly solved, and I substitute this root for b.
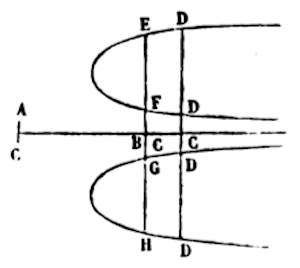
If the said value is empty, it is only if in the solved equation there are no terms unless they are multiplied by x or y, so in y3 – axy + x3 = 0; then I select the terms (-ax + x3) in which x separately and even y separately, if another multiplied by x is of minimum dimension. And this gives + xx/a for the quotients of the first term, and xx/a + p for y is substituted. In y3 – a2y +axy – y3 = 0, the quotient of the first term is permitted, or one can draw it out from – a2y – x3, or from y3 – a2y. If this value is imaginary, so in this, y4 + y2 – 2y + 6 – x2y2 – 2x + x2 + x4 = 0, I increase or diminish the quantity x as long as the said value remains unreal. Thus in adding this schemata, with AC (x) being nothing, then CD (y) is imaginary.
But if AC diminishes by giving AB, x should go up to BC; then I posit what BC (x) has none of: CD (y) will be a value quadrupled (CE, CF, CG, or CH), and anything can be the quotient of the first term, just as the surfaces BEDC, BFDC, BGDC, or BHDC may be designated. In similar cases, if you are stumped, this method will untangle you.
Finally, as proof of this power, x or y should be fractional, and so I reduce it to an integral: so in this example y3 – xy1/2 + x4/3 = 0. I make y1/2 = v, and x1/3 = z, which results in v6 – z3v + z4 = 0, of which the root is v = z + z3, etc. or (restoring the values) y1/2 = x1/3 + x, etc. and I make y = x2/3 + 2x4/3 square, etc.
Investigating the curved areas would be frequently sufficient. More correctly, with any problem of curve lengths, of solid quantity and surface, moving down towards a center of gravity can, in tandem, be reduced to searching for quantities of the surfaces of the final, flat line, and no work will similarly be added. On the other hand, those of yours which I use only require the method to be briefly discussed.
Applying the Above to the Last of Such Equations
Suppose we have any curve ABD, and a rectangle AHKB in which sides AH or BK is one. And the known straight line DBK moves uniformly towards AH, tracing out the areas ABD and AK; and where BK (1) is the moment of any AK (x) and BD (y) the moment of any gradually enlarging ABD; and which from the moment BD, area ABD perpetually gives, possibly according to the previously mentioned rules, area ABD, thus finding its tracing, or with (1) AK (x) moment 1 conferring what had been traced.
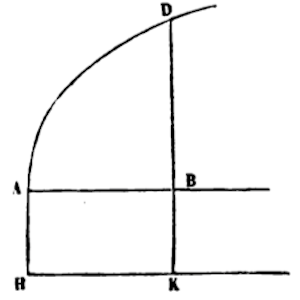
*N. B. This method is described by Fluxions (Fluentes) and their Moments. These are later called Moments by Mr. Leibniz and further named : Methodi Differentialis. [Area.] Interpolation.
9.
Now by any ratio, the surface ABD is continuously given from its moment, eliciting and similarly drawing out, by the previously mentioned rules, whatever other quantities from its moment are so given. An example will make it clearer.
Finding Curved Lengths
Let ADLE be a circle with arc AD to be found. I conceive tangent DHT, and I tentatively fit in a small rectangle HGBK, and make AE=1=2AC. †
Let the moment with base AB(x) go to BK or GH, to HD let go the moment of the arc AD::BT: DT :: BD (sqrt(x-xx)) : DC(1/2) :: 1(BK): ½ sqrt(x-xx) (DH).
Indeed ½ sqrt(x-xx) or sqrt(x-xx) / 2x-2xx is the moment of the arc AD. Reducing, we have 1/2x-1/2 + 1/4x1/2 + 3/16x3/2 + 5/32x5/2 + 35/256x7/2 + 63/512x9/2, etc. And so the length of the arc AD is, by the second rule, x1/2 + 1/6x3/2 + 3/40x5/2 + 5/112x7/2 + 35/1152x9/2 + 63/2816x11/2 etc. or x1/2 in 1 + 1/6x + 3/40x2 + 5/112x3 + 35/1152x4 + 63/2816x5, etc.
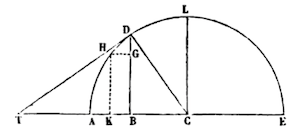
No differently, I make CB x and root CA 1, the found arc LD is x + 1/6x3 + 3/40x5 + 5/112x7, etc.
What shall be observed is thus unity: surfaces with solids, lines with surfaces, and points with lines are driven for any designated moment (as in this example).
Fearing neither unity being spoken of in a point, or infinitely small lines, if there are now certainly proportions for the geometer to contemplate, it is because one makes use of indivisible methods.
Hence should be made a conjecture upon surfaces and by quantities of solids, and of centers of gravity.
Finding the Above Conversion
Indeed derived from the area or even length, or otherwise etc. Any given curve or length of the desired base AB, are found by the extraction of the root of x from the equation by the preceding rules.
† Example of the calculus by moments of fluxions.
Finding the Base from the Given Area
Even if out of the area ABDC there is a hyperbola (1/1+x = y), divided by any base AB, and the area is named z, I extract this root z (ABCD) = x – 1/2x3 + 1/3x3 – 1/4x4 etc. neglecting the term in which x is of multiple dimensions, that is when we seek z in the quotient.
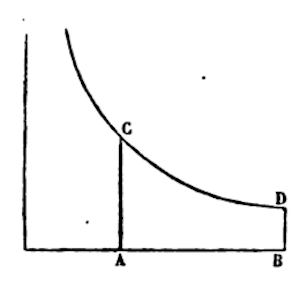
Even if so wished, because z goes up to as many as five dimensions, I neglect every -1/6x6 + 1/7x7 – 1/8x8, etc. and I extract as much as 1/3x3 – 1/4x4 + 1/3x3 – 1/2x2 + x – z = 0.

So that you may see the analysis, I shall present it by noting two sequences.
Because they may be substituted among themselves, I always omit any of these terms with no foreseen use hereafter. This will be a rule, since after the first term, I do not add multiple terms of any quantity on the right by some collateral result, when unity stands out from the index of dimensions to the index of the maximum dimension. In order that in this example, when the maximum dimension is 5, I omit every term after z5, after z4 I put only one, and two after z3. With the root extracted, everywhere (x) is equal, or of unequal dimension, this will be the first rule; because after the first term, from any quantity itself, I do not add multiple terms to the collateral result on the right, as much as the index of dimensions of the index of the maximum dimension are each standing as unity for this first term. Or even terms of unity, if the indices of the dimension x are unity everywhere, a third stands out by turns, and thus remains. When I see that p, q, or r, etc. in the newly resulting equation are joined in so many dimensions, this is the same value of the remaining quotients of the terms I've added by the desired division. This is done so that you may see.
Finding the Base from the Given Curve Length
If from the given arc (alpha)D one traces a sinus, AB; by the equation z = x + 1/6x3 + 3/40x5 + 5/112x7, etc. found above, (I certainly put AB = x, (alpha)D = z, and A(alpha) = 1), the extracted root will be x = z -1/6z3 + 1/120z5 – 1/5040z7 + 1/362880z9, etc.
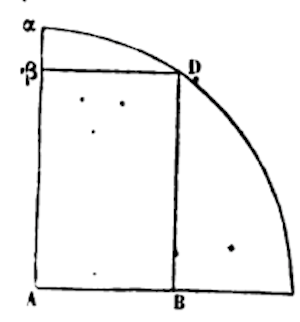
And thereafter, if the cosine Aβ is given (cupis) from this arc, this makes Aβ(=sqrt(1-xx)) = 1 – 1/2z2 + 1/24z4 – 1/720z6 + 1/40320z8 – 1/3628800z10, etc.
Progression of the Series Continued
Should it be observed that 5 or even 6 of the terms you mention can be seen as roots, from the observed analogy they could generally be produced arbitrarily.
So with this x = z + 1/2z2 + 1/6z3 + 1/24z4 + 1/120z5, etc. that you produce, I divide the final term by this succession of numbers: 2, 3, 4, 5, 6, 7, etc.
And for this x = z – 1/6z3 + 1/120z5 – 1/5040z7, etc., by these: 2 X 3, 4 X 5, 6 X 7, 8 X 9, 10 X 11, etc.
And this x = 1 – 1/2z2 + 1/24z4 – 1/720z6, etc., by these: 1 X 2, 3 X 4, 5 X 6, 7 X 8, 9 X 10, etc.
And for this z = x + 1/6x3 + 3/40x5 + 5/112x7, etc., I multiply by these: 1 X 1 / 2 X 3, 3 X 3 / 4 X 5, 5 X 5 / 6 X 7, 7 X 7 / 8 X 9, etc. And so follow the rest.
The Preceding Application for Mechanical Curves
And so that of geometrical curves stands sufficient. Now such method of ours by no means rejects the curve, although mechanical.
Take for example the (Trochoides), ADFG, with vertex A and axis AH and AKII, you rotate by tracing it out. And the surface ABD should be found. Now I put AB = x, BD = y, as above, AH = 1; The first length to find is BD. Indeed, from the nature of the (Trochoidis) KD = arc AK. Whereby all of BD = BK + arc AK. Because BK is (= sqrt(x -xx)) = x1/2 = 1/2x3/2 – 1/8x5/2 – 1/16x2/2 etc.and (from the aforementioned) arc AK = x1/2 + 1/6x3/2 + 3/40x5/2 + 5/112x7/2, etc. Therefore, all of BD = 2x1/2 – 1/3x3/2 – 1/20x5/2 – 1/56x7/2, etc. (by rule 2) area ABD = 4/3x3/2 – 2/15x5/2 – 1/70x7/2 – 1/252x9/2, etc.
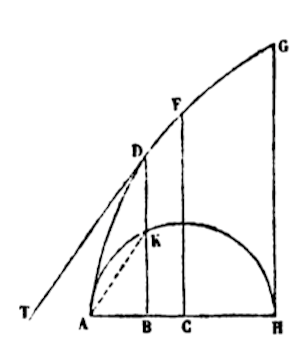
Or even more briefly: with straight line AK and tangent TD parallel, we have AB to BK as the moment of line AB to the moment of line BD, which is x: sqrt(x – xx) ::1:1/x sqrt(x – xx) = x1/2 – 1/2x1/2 – 1/8x3/2 – 1/16x5/2 – 5/128x7/2, etc. Whereby (by rule 2) BD = 2x1/2 – 1/3x3/2 – 1/20x5/2 – 1/56x7/2 – 5/576x9/2, etc. And the surface ABD = 4/3x3/2 – 2/15x5/2 – 1/70x7/2 – 1/252x9/2 – 5/3168x11/2, etc.
This is not unlike the way (by placing C at the center of the circle, and CB = x) you obtain the area of CBDF, etc.
Let there be an area ABDV of quadrature VDE (in which the vertex is V, and A is the center of the interior circle VK fitted within) for which we search. Draw out any AKD, and I make DB, DC, KG point downward. Let it be that KG:AG::AB(x):BD(y), or xXAG / KG = y. True to the nature of a quadrature is BA (=DC) = arc VK, or VK=x. Whereby I put AV=1, and let GK = x -1/6x3+1/120x5, etc., clearly from the above, and GA=1 – 1/2x2 + 1/24x4 – 1/720x6, etc.
Indeed y (=x X AG/ KG) = 1 – 1/2x2 + 1/24x4 – 1/720x6, etc. / 1 – 1/6x2 + 1/120x4 – 1/5040x6, etc. or dividing, y = 1 – 1/3x2 – 1/45x4 – 2/245x6, etc. and (by rule 2), area AVDB = x -1/9x3 – 1/255x5 – 2/6615x7, etc.

So the length of the quadrature permits difficult calculations, is determinable.
Nor do I know this method because this method, in varied ways, does not extend itself. On the contrary, tangents of mechanical curves (if it were to make none other) the power of which may be considered. And any common analysis by equations from finite, constant numerical terms (when possible) finishes, along with equations that are always infinite: in order to remove any doubt of the name of the analysis now just like this division. Reasoning by this happens indeed, not without being fixed by it, nor by less exact equations; they permit any of these terms, that neither our fellow human beings (homines) and finite reason nor their designation, nor our ability to understand, quantities henceforth desired for attaining exact acquaintance: just as neither surd roots of finite equations, nor numbers, nor whatever analytical art we may so be able to exhibit, for any quantities to separate any of the remaining by exact recognition.
Finally, I merit extending my supposition up to this analysis for the benefit of the curved area and length etc. (if only should they be) * exact and geometrically
N. B. Quadrature curved by infinite equation, which sometimes terminating and finite, it avoids. (1) [ Also explained in Prop. V Libri de Quadraturis. And I propose these point down by the preceding four. So while the method of fluxions and moments, to what point does it have in the five propositions of the book of quadratures (Libri de Quadraturis) of Newton made known in 1669.] Addition.
determined. As I shall speak of yours not its location. I will return to these two before demonstrating the remaining which come to mind.
Demonstration of the simple curved quadrature in the first rule.
Preparing to demonstrate the first rule.
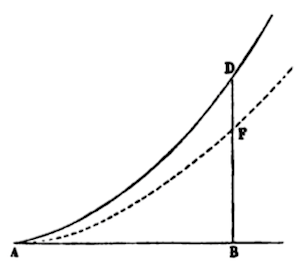
† So let any curve ADδ with base AB = x, and have applied to it a perpendicular BD = y, and area ABD = z, to the front. Similarly let Bβ = 0, BK = v, and rectangle BβHK (ov) equal space BβδD.
Therefore Aβ = x + 0, and A(unknown symbol) = z + ov. These will have been moved forward, from the relation between x and z to the arbitrary assumption sought as p, you see any of the following now.
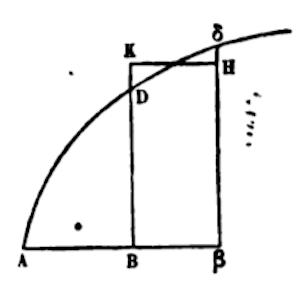
How pleasing it is to suppose 2/3x3/2 = z, or 4/9x3 =zz. * Then x + o (A[β]) for x, and z + ov (A[δ][β]) is substituted for z, producing 4/9 in x3 + 3x2o+ 3xo2 + 03 = (from this curve will be born) z2 + 2zov + o2v2. And by bearing (4/9x3 and zz) equally, remaining divided by o, is 4/9 in 3x2 + 3xo + o2 = 2zv + ov2.
If now I suppose Bβ infinitely diminishing and vanishing, or o is nothing, v and y will be euqal, and terminated by o repreatedly vanishing, whereby 4/9 X 3xx remains = 2zv, or 2/3xx(=zy) = 2/3x3/2y, or x1/2 (= x3/x3/2) = y. Whereby by the opposite if x1/2 = y, we write 2/3x3/2 = z
Demonstration
Or even generalizing, if n / m + n X axm+n /n = z or if I put na/m + n = c, and m + n = p, if cxp/n = z + oy) I substitute for z, producing cn in xp + poxp-4, etc. = zn +/- noyzn-1; etc. indeed the remaining terms, so many which vanish, I omit. Now bearing cnxp and zn equally, dividing the remaining by o, leaves cnpxp-1 = nyzn-1 ( = nyzn/z = nycnxp/cxn/n) or I divide by cnxp, letting px-1 = ny / cxp/n or pcxp-n/n = ny, or even, I recover na/m + n for c, and m + n for p, that is, m for p -n, and na for pc, making axm/n = y. Whereby from the opposite, if axm/n = y, let n / m +n axm+n/n = z. Q. E. D.
Finding Curves which can be squared.
Now, in passing, the method for any curve should be noted pleasing: for any recognized area, * it can be found. Certainly I still may begin many equations for the relation between the area z and the base x, until then searching for the application of y. In order that we may suppose sqrt(aa + xx) = z, from performing a calculation, we find x / sqrt(aa + xx) = y. And so it is left.
Demonstrating the Solution to the affected equation.
The next demonstration is literally the equation leading to the solution. Certainly, which quotients, with x are barely sufficient, any wise revelation is wise until it nears truth, in order that defects (p, q or even r, etc.) match up to the exact value of this y, as much as the lesser avoids giving any quantity whatsoever, and which is infinitely produced from it equal to this y. This so stands.
Since, from the last term of the equation, any p, q, r, etc. are roots, quantities in which x has minimal dimensions (that is, how much smaller is this last term, if I suppose x is barely sufficient); in any continuous operation they are raised : the final term (by 1. 10 Elem.) the lesser avoids as much any given quantity, and entirely vanishes if the thing infinitely continues.
Certainly, if x = ½, let x be half of every x + (gamma)3 + x3 + x4, etc. And x2 is half of every x2 + x3 + x4 + x5, etc. And so if x > ½, let x be more so half of every x + x2 + x3, etc. And x2 even more so half of every x2 + x3 + x4, etc. So if x/b > ½, let x be yet more so half of every x + x3/b + x3/bb, etc. And so on. And the coefficients of
*This proposition from equations of fluxions involves finding the fluxions.
numbers which (attmet), this generally perpetually decreases, or when it increases, so much goes up to what are, until now, these other substitutions.
If any of the final terms of the equation continue to diminish as long as just as many vanish, a single one from the root will diminish, as long as the last term similarly vanishes. Whereby quantities p, q, r, etc. or one continuous value decreases as long as there are so many, it thoroughly vanishes with the thing being given to infinity. Because a single one of your values p, q, or even r, etc. with quotients so far, adequately extracts the roots of the proposed equations ( So in the solution to the equation y3 + aay + axy – 2a3 – x3 = 0 as shown above, you will perceive y = a + p = a – 1/4x + q = a – 1/4x + xx/64a + r, etc.) Whence the proposition is sufficiently proved because the infinite quotients of the product are unity from the values of y.
Similarly, the substitution of the quotients for y in the proposed equation stands. You will see, namely, that these terms are continually destroyed when x is of minimal dimension.